E-Archive
Science Update
in Vol. 17 - November Issue - Year 2016
Developments in Residual Stress Measurement by X-ray Diffraction
Diffraction occurs when there is a constructive interference of scattered x-rays from atoms arranged periodically in a crystalline material (crystal)

Identifying the residual stress of a gear utilizing the technology of an x-ray diffraction measurement system
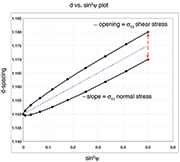
The sin2? measurement technique is a common XRD technique used to measure residual stress
Introduction
The importance of residual stresses in the manufacture and use of engineering components is indisputable. They influence subsequent manufacturing operations, and can affect service life in certain mechanical and chemical environments. Fortunately, potentially damaging Residual Stresses can be managed and beneficial residual stresses can be installed by using controlled thermal and mechanical processes. Analysis of residual stresses requires quantitative data, which in turn requires credible, convenient and reliable tools to measure surface and internal stress. These tools are also available to monitor and assure the quality of parts manufactured with engineered surfaces.
The measurement of residual stress by X-ray diffraction is supported by detailed and complex mathematics. None of that mathematical support will appear here, but some of its implications will be mentioned. Readers who wish to know more about residual stress, its measurement and its management are encouraged to consult an equipment manufacturer or another experienced expert for further information.
Stress and Strain
Stress is a measure of mechanical force acting over a given cross-sectional area, and cannot be measured directly. Stresses due to applied forces can be calculated, provided the magnitude and direction of the forces and the details of the component are known. Residual stresses are, by their nature, due to forces contained within and reacting within the component. These forces are in balance in the component, and are locally additive with forces resulting from external loads.
Strain represents the component's response to stress. It is measured as the change in a dimension per unit length.
If a mechanical load is applied axially to a test piece having a uniform cross section, the test piece will initially stretch elastically, by an amount proportional to the load. As the test piece elongates, its width and thickness are reduced, by an amount determined by a material constant, Poisson's Ratio. When the load is removed, the test piece will return to its original dimensions. Knowing the cross-sectional area of the test coupon and the loads applied allows the stress (force per unit area) to be calculated. Similarly, the extension of the test piece compared to its original length allows the corresponding strain to be calculated. Given that the relationship between stress and strain is initially linear, the proportionality constant can be calculated. This is the Elastic Constant, or Young's Modulus, and it represents the bulk material.
If the test coupon is extended beyond the linear range, it will not return to its original length when the load is removed. It is said to be plastically deformed. If the Elastic Constant of that coupon is determined again, its value will be found to be unchanged. The Elastic Constant of a material is independent of its deformation history.
Residual Stress and X-ray Diffraction
The gauge length over which elastic strain is to be measured can be very small. The most widely used method of measuring residual stress, based on the diffraction of X-rays, uses the distance between planes of atoms in the crystals that make up almost all solid materials to measure strain, from which stress is calculated.
The X-rays used in these measurements have relatively low energy, which limits their penetration into the surface of the part under examination. The depth of penetration depends on the ability of the sample's material to absorb the X-rays, and the geometric arrangement of the instrument itself. X-ray intensity diminishes exponentially with distance travelled within the material, so the greater contribution is from closer to the surface. Typically, each measurement represents material within about 0.0005 inches of the surface. These layers are so thin that the external perpendicular force acting on the free surfaces can be considered to be zero.
Spatial resolution is determined by the geometry of the X-ray beam. The size and shape of the beam is determined by the choice of collimators. The selection of beam size is important in limiting the irradiated volume to the feature to be measured, while being large enough to allow an adequate number of crystal orientations to be present in the irradiated volume.
One of the conditions for X-ray diffraction to occur was that the angular relationship between the incident and diffracted beams must satisfy the Bragg equation, n?=2dsin?. The wavelength of the X-rays is "?", the distance between adjacent planes of atoms in the material of the poly-crystalline sample is "d", and "n" is an integer, allowing there to be multiple orders of diffraction. The diffraction angle "?" is half the angle between the transmitted beam and the diffracted beam.
As the Bragg equation indicates, θ is most sensitive to small changes in the crystal plane spacing when the diffraction angle is large. A range of wavelengths is available in the characteristic X-ray spectral lines of the transition metals. The selection of an X-ray tube target giving a detectable diffraction pattern at the highest available diffraction angle is as important now as it was when the first measurements were performed.
The first measurement of Residual Stress by X-ray diffraction was carried out in 1925, only a few years after the mathematical description of the diffraction process was developed by William Lawrence Bragg and his father William Henry Bragg.
The development of instruments for residual stress measurement by the X-ray diffraction method has been in a series of steps, not necessarily linked to developments in conventional X-ray diffraction techniques as a whole. In some cases, a concept has had to wait for many years before an advance in some aspect of the equipment allowed the idea to be commercialized.
Within the material, the distributions of stress and strain can be described mathematically. If we can measure the near-surface stress in two directions, we can calculate the stress in a related direction on the surface. Unlike stress, strain can be measured relatively easily. We simply need to measure the elastic change in a known, related direction. The simplest expression for strain is ε = (d1-d0)/d0, and with a given set of geometric features of the instrumentation and measurement parameters, we can include them in an Elastic Constant specific to that set-up. This is done by determining an X-ray Elastic Constant, combining the properties of the material with parameters associated with the X-ray method during a mechanical test. The "unstressed" lattice plane spacings, d0, are obtained from crystal planes containing the stress axis, and values of d1 are obtained from planes with a known angle, tilted towards the stress axis.
The earliest X-ray diffraction measurements of residual stress (using the single exposure method) would probably have used glass photographic plates to record the diffraction patterns, in an arrangement rather like a back-reflection Laue photograph, but using filtered radiation. For residual stress measurement, this rigid, stable but fragile medium would have been excellent. There would have been difficulties in determining the precise locations of broadened peaks, and in comparing them with peaks showing un-broadened k-alpha doublets.
In a further simplification, calculation of the actual lattice plane spacings could be eliminated, and the stress calculated simply from the angular peak shift between un-tilted and tilted exposures, again with an appropriately determined Elastic Constant.
The development of flexible photographic film allowed the cameras of the day to place narrow strips of film on an arc attached to the collimator, curved to centre on the origin of the diffraction pattern. Fiduciary marks were placed on the films, either by masking them to produce sharp shadows at known locations, or by including a well-defined diffraction pattern from an unstressed powder prior to developing the film. These steps were needed to provide reference points from which measurements of peak shift could be made, and to make allowance for dimensional changes in the film itself during processing.
Diffractometer Measurements
A step-change in X-ray diffraction methods occurred with the introduction of the Diffractometer. Designed to provide numerical data of diffracted intensity as a function of 2-theta, the basic diffractometer would illuminate a rectangular area of the flat specimen with an angle of incidence theta, and a detector positioned at 2-theta would receive the diffracted X-rays. The amplified output of the detector was recorded as a series of pulses to scalars, rate-meters and chart recorders. The X-ray optics of basic diffractometers were not well suited to stress measurement, but modified diffractometers were used to successfully measure residual stresses in 1953.
Having a numerical description of the X-ray peaks allowed the development of calculation methods for peak position, and allowed known distortions of diffraction data to be corrected more readily. The ready availability of numerical data also enabled the adoption of the "Multiple Exposure Technique". There is a linear relationship between strain and the square of the sine of the tilt angle "psi" used in measurements of residual stress. Strain, and hence stress, can be determined from the slope of that linear relationship. The measurements made earlier, using the techniques described above were based on only two points on that line, at Psi = 0 degrees, and one other value. Each measurement relied on only a small segment of the available strain data. The new technique could take advantage of a full range of positive and negative tilt angles, and do so with the optimum choice of radiations to maximize peak shift. Fitting the line to the data allowed routine calculation of the quality of the fit, and investigation of outlying data-points could reveal the sources of errors.
Returning to Film-like Methods
During the late 1970s, a breakthrough was made in the design of X-ray detectors. The Position Sensitive Proportional Detector could detect the full profile of an X-ray peak and its surrounding background, without the necessity of stepping or scanning the diffractometer through the profile.
It was not long before the new linear detectors replaced the film in cameras otherwise similar to the early designs used for residual stress measurement. Mounted on arcs attached to the X-ray tube mounts, and aimed at the same point as the collimator, the position sensitive proportional counters with their associated power supplies and pre-amplifiers probably dominated the instruments. Now, the simplicity of the film-based methods could adopt the sophistication of the numerical methods applied to diffractometer measurements.
In the 1990s, a new type of linear X-ray detector became available. The Position Sensitive Scintillation Detector consists of a layer of a scintillation material mounted on one end of a coherent fiber optic bundle. An X-ray photon striking the scintillator releases a flash of light at the inner surface, which is transmitted to the other end of the bundle, where the light is amplified in an array of photomultipliers and stored as accumulated charge in an array of CCDs. The accumulated charges are digitized periodically, and accumulated numerically in an array of data matching the face of the detector. Separating the detector from the electronics dramatically reduced the size and weight of the goniometer assembly.
The latest linear detectors available replace the scintillation detector by a linear array of photon counters, with a USB connection to the controlling computer. These detectors are capable of handling greater count rates; they simplify the construction of machines, and are small enough to permit large tilt angles to be used for measurements where peaks are available at favourably high diffraction angles.
Other innovations that have entered the market are based on attempts to miniaturize and simplify system operation. Examples of this include the cosine alpha technique, which, while simplifying the measurement technique, has yet to be assessed fully in round robin testing, where samples are circulated and measured repetitively to establish repeatability and reliability. Unfortunately, some of these new methods have not yet been subjected to rigorous comparison testing of this type, and may have severe limitations when measuring materials that are not completely isotropic and homogeneous.
Current Instruments and Applications
Residual stress measurement is a tool for practical engineering and manufacturing environments, as well as for use in a laboratory setting. As a result, instruments for residual stress measurement tend to be robust, and may be found in variants that can be installed on an automated manufacturing line, or taken to a job site, be it in a factory, on a bridge being assessed for future serviceability, or at a pipeline under construction.
In their most recent variants, portable machines of the current generation of can be packed into a single case for ease of transportation and operated from a car battery through the use of a commercially available inverter. They may use low-power X-ray tubes which can be air-cooled., or have self-contained cooling systems for their high-voltage power supplies and X-ray tubes. Yet these machines are complementary to the sophisticated and powerful instruments designed for laboratory use.
For Information:
Proto Manufacturing Ltd.
2175 Solar Crescent, Oldcastle, Ontario
Canada, N0R 1L0
Tel. +1.519.737.6330
Fax +1.519.737.1692
E-mail: proto@protoxrd.com
www.protoxrd.com




























