E-Archive
Off the Beaten Track
in Vol. 19 - January Issue - Year 2018
Much Ado About Nothing

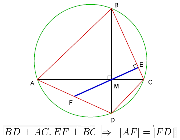
Brahmagupta´s theorem on cyclic quadrilaterals
"As the sun eclipses the stars by its brilliancy, so the man of knowledge will eclipse the fame of others in assemblies of the people if he proposes algebraic problems, and still more if he solves them."
****
Thus wrote Brahmagupta, an Indian astronomer and mathematician born in the year AD 598. His father was an astrologer and, as a child, Brahmagupta became accustomed to scrutinizing the movement of the stars and the planets. These studies led him to consider the importance of numbers and to study the relationship among bodies in space, encouraging him to develop his own ideas concerning geometry and astronomy. Although he considered himself primarily an astronomer, Brahmagupta’s contributions to mathematics far exceed his other accomplishments.
At the age of thirty, Brahmagupta wrote his most famous work, a book entitled Brahmasphutasiddhanta (syllabized Brahma-sphuta-siddhanta), translated as Correctly Established Doctrine of Brahma. It was a theoretical treatise consisting of twenty-four chapters and, as was the custom among Indian scholars in that period, it was written as a poem in elliptical verse in Sanskrit with a total of 1,008 verses.
The first ten chapters cover astronomical topics such as mean and true longitudes of the planets, lunar and solar eclipses, risings and settings of the planets, the Moon’s crescent and shadow and the conjunction of the planets with each other and with the stars. Going against the established doctrines of his academic peers, Brahmagupta stated that the Earth was a sphere and that its circumference was about 36,000 km, only 4,000 km less than the actual circumference. He also demonstrated that the Earth is closer to the Moon than it is to the Sun by detailed observation of how the Sun illuminates the Moon.
In the second part of his book, Brahmagupta presented extremely influential concepts to basic mathematics, algebra, geometry, and trigonometry. He applied mathematics and algebra in describing and predicting astronomical events. Above all, he was the first person in history to introduce the use of zero in mathematical calculations. Nowadays it seems obvious to us that zero is a number in its own right, but that was not true in the past. The Babylonians had invented a placeholder digit with no practical function, whereas Ptolemy and the ancient Romans had devised a symbol to denote a lack of quantity, also defined as “nothing”. Brahmagupta defined zero as the number obtained when a number is subtracted from itself and also stated that zero divided by any other number gives zero. He was the first to give rules for calculations that apply to zero and to describe arithmetic manipulations with negative numbers.
In other chapters of his book, Brahmagupta described algorithms for multiplications, solutions of linear and quadratic equations, square roots and how to compute sines. He even considered systems of simultaneous equations and solving quadratic equations with two unknowns, something that would be studied in the West only a thousand years later.
Brahmagupta's greatest achievement in the field of geometry is his formula for cyclic quadrilaterals. Known as “Brahmagupta’s Theorem”, this formula allows the exact calculation of the figure’s area, given the lengths of the sides of any cyclic quadrilateral.
In 665 Brahmagupta moved to Ujjain, where he was named director of the local astronomical observatory. There he wrote his second most famous book, the Khandakhadyaka, a practical manual of astronomy. In this work, Brahmagupta gave the length of the year with a surprising degree of accuracy: 365 days, 6 hours, 12 minutes and 36 seconds.
A few years after Brahmagupta’s death, northwestern India was conquered by the Arab Caliphate based in Baghdad. The Caliph Al-Mansur was a strong supporter of scholarly research and organized the translation of works from other cultures. He received the visit of an Indian astrologer called Kanaka, who brought with him several Indian astronomical texts, including the two works by Brahmagupta. These were immediately translated into Arabic.
Almost a century later, a Persian mathematician called Al-Khwarizmi wrote a book entitled Addition and Subtraction in Indian Arithmetic based on Brahmagupta’s works. Interestingly, the word “algorithm” derives from the name Al-Khwarizmi, while the word “algebra” derives from the Arabic “al-jabr”, one of the two types of operations that Al-Khwarizmi used to solve quadratic equations.
Al-Khwarizmi’s work was translated into Latin in the twelfth century and was used as the main mathematical textbook in European universities until the sixteenth century. Thanks to this translation, the decimal positional number system invented by Brahmagupta spread throughout the world.
By Giovanni Gregorat, Contributing Editor MFN
Author: Giovanni Gregorat



























